ggga¶
Synopsis¶
from ggga import *
import asyncio
import numpy as np
# 1. Define the parameter space we want to optimize.
# Here, a R² space.
space = Space(
Real('x1', -2, 2),
Real('x2', -2, 2))
# 2. Define the objective function we want to optimize.
# Here, the Goldstein-Price function with some noise
# and a log(y+1) transformation of the value.
from ggga.benchmark_functions import goldstein_price
async def objective(x, rng):
y = goldstein_price(*x)
y_with_noise = y + rng.normal(scale=10)
while y_with_noise < 0:
y_with_noise = y + rng.normal(scale=10)
value = np.log(1 + y_with_noise)
cost = 0.0
return value, cost
# 3. Choose optimization settings.
minimizer = Minimizer(
max_nevals = 50,
)
# 4. Kick of the optimization.
# The result contains all evaluations
rng = RandomState(1234) # choose seed for reproducibility
loop = asyncio.get_event_loop()
res = loop.run_until_complete(minimizer.minimize(
objective, space=space, rng=rng))
# 5. Visualize the result.
from ggga.visualization import PartialDependence
fig, _ = PartialDependence(model=res.model, space=space, rng=rng) \
.plot_grid(res.xs, res.ys)
fig.savefig("README_example.png")
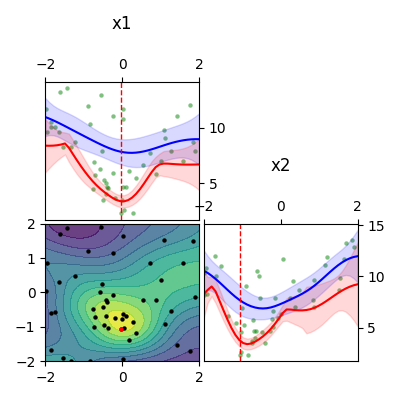
The visualization shows all samples and the response surface of a Gaussian Process Regression fitted to those samples. The optimum of the Goldstein-Price function is at (0, -1). Each column shows one parameter (x1 and x2), in between them the interactions between the parameters with a contour plot. The individual parameter plots view the surface from one side. The blue line is the average value of the surface along that parameter, with a ±2σ region around it. The red line is the minimal value of the surface along that parameter, also with a ±2σ region. The best sample is marked with a dashed line (individual plots) or a red dot (interaction plot). However, the best found sample might not be at the optimum, due to noise.
Example objective function that runs an external program:
async def objective(x, rng):
# set up the command to execute
# like: `./someprogram --x1=1.978 --x2=-0.471`
command = ['./someprogram']
for param, value in zip (space.params, x):
command.append(f"--{param.name}={value}")
# run the command
process = await asyncio.subprocess.create_subprocess_exec(
*command, stdout=asyncio.subprocess.PIPE)
out, err = await process.communicate()
# parse the output
value = float(out.decode().splitlines()[-1])
cost = 0.0 # or could measure CPU-time
return value, cost
Description¶
GGGA is an optimization algorithm that combines evolutionary algorithms with Bayesian optimization. It is suitable for optimizing expensive black-box functions with noise. In particular, it may be used for hyperparameter tuning of machine learning algorithms.
Related work:
scikit-optimize: an implementation of Bayesian optimization, implemented in Python.
irace: a parameter tuning tool using iterated racing, implemented in R.
Installation¶
GGGA requires Python 3.6 or later, and an up to date Scipy stack (numpy, scipy, matplotlib, pandas, scikit-learn).
Installation can be performed directly from the GitHub repository:
$ pip install git+https://github.com/latk/ggga.py.git
Alternatively, build the container from the Dockerfile.
Examples¶
The ggga module is also a command line tool
to explore various benchmark functions.
By default, GGGA is compared to random samples.
$ python3 -m ggga --help
Run the example from the Synopsis:
$ python3 -m ggga goldstein-price --logy --samples=50 --noise 10
Example optimization strategies¶
The example runner can receive a number of optimization strategies to compare.
These can be selected and configured on the command line.
To configure a strategy, provide a YAML document with type tags,
e.g. !GGGA { ... }.
random: take random samples.ggga: use GGGA for optimization.!GGGA { ... }: use GGGA for optimization. The mapping may provide extra arguments for theMinimizer. The Minimizer’s nevals and surrogate_model_class arguments should be specified via the example runner’s –samples and –model flags. All acquisition strategies can be specified through YAML.!Irace { ... }: use irace for optimization.port: int. Required for communication between the objective function and irace.
parallel: int = 1. How many evaluations may be performed in parallel.
digits: int = 4. Internal precision used by irace.
min_racing_rounds: int = 2. Racing rounds before the first statistical test is applied. By default, irace uses 5 rounds here.
confidence: float = 0.95. Confidence level for the statistical test during racing.
Stability Policy¶
The API is unstable and may change at any time without prior notice.
Acknowledgements¶
Development of this software was supported by the Workgroup for Network Security, Information, and Data Security at the Frankfurt University of Applied Sciences (GH: @fg-netzwerksicherheit, Homepage: Forschungsgruppe für Netzwerksicherheit, Informationssicherheit und Datenschutz)
License¶
Copyright 2018 Lukas Atkinson
GGGA is licensed under the terms of the AGPLv3+, see the LICENSE.txt for details.